生成AIの進化は止まることを知らず、GoogleのAIサービスも新たなフェーズに突入しました。これまでの「Gemini Advanced」という名称は廃止され、現在は「Google AI Pro」および「Google AI Ultra」という新プラン体系に刷新されています。
しかし、選択肢が増えたことで「ProとUltraは何が違うの?」「無料版のGemini Flashで十分では?」と迷ってしまう方も多いはずです。
以下のような疑問をお持ちではないでしょうか?
- 上位プラン「Google AI Ultra」との決定的な差は?
- 「Google AI Pro」を選ぶべき明確な理由は何か?
- 各プランごとの制限などは?
この記事では、以下の内容を詳しく解説します:
- Google AI Proを含む3つのプラン(無料・Pro・Ultra)の完全比較
- Google AI Proがコスパ最強の理由
- あなたに最適なプランの選び方と判断基準
この記事を読み終わる頃には、複雑になったプランの違いがクリアになり、あなたの用途に最適なGoogleのAI環境を選択できるようになるはずです!
内容をまとめると…
プランは無料プラン・Google AI Pro・Google AI Ultraの3つ
無料プランはあくまでお試し用
Google AI Proがコスパ最強のプラン
コツを掴み活用すればGoogle AI Proの機能でも、十分副業として収益を得ることが可能。
romptn ai編集部が厳選しておすすめする完全無料のAI副業セミナーでは、副業で収入を得たり、昇進・転職などに直結させるさらに深い生成AI活用スキルを学ぶことができます。
今だけ期間限定で無料セミナー申込者には、必須で知っておきたいAI知識をまとめた12大特典を無料プレゼント中です!
まずは無料受取期間が終わる前に、お気軽に下記のボタンからフォームを入力して無料特典を受け取ってください!
○ 無料プレゼント内容












\ 受講者数20万人突破の大人気セミナー /
Google AI Proとは?
まず、混乱しやすい現在のGoogle AIのプラン構成について整理しましょう。以前の「Gemini Advanced」プランは廃止され、現在は用途に合わせて以下の3つの段階に分かれています。
- 無料プラン(Free):手軽にAIを試せるエントリーモデル。
- Google AI Pro(標準有料プラン):高性能なAIを日常的に使いこなすためのスタンダードプラン。
- Google AI Ultra(最上位プラン):ヘビーユーザーやプロフェッショナル向けの最上位プラン。
各プランの大まかな違いは、使用できるAIの回数制限、動画生成機能などの各種機能の利用可否、ストレージ容量などがあります。以下ではそれらの違いをより詳しく見ていきます!
【徹底比較】無料・Google AI Pro・Google AI Ultraの比較表
「自分はどのプランを選ぶべきか」を判断するために、3つのプランを一覧表で比較します。以下は各種プランの重要ポイントの比較表になります。
| 比較項目 | 無料プラン | Google AI Pro | Google AI Ultra |
| 対象ユーザー | ライトユーザー、日常的な検索・要約 | 一般的な個人ユーザー、クリエイター、プログラマー | 業務用、企業、チーム、高セキュリティが必要な組織 |
| 月額料金 | 0円 | 2,900円 | 36,400円 |
| 搭載AIモデル | Gemini Flash・Pro | Gemini Flash・ Pro | Gemini Flash・ Pro |
| Googleアプリ連携 | ×利用不可 | 〇利用可能 | 〇利用可能 |
| Gemini Proの回数制限 | 1日5回まで | 1日100回まで | 1日500回まで |
| 画像生成 | 1日100枚まで利用可能 | 1日1000枚まで利用可能 | 1日1000枚まで利用可能 |
| 動画生成機能 | ×利用不可 | 〇1日3本まで利用可能 | 〇1日5本まで利用可能 |
| AIクレジット | 付与なし | 毎月1,000クレジット付与 | 毎月25,000クレジット付与 |
| ストレージ特典 | 15GB | 2TB | 30TB |
| エージェントモード | ×利用不可 | ×利用不可 | 〇利用可能(1日200回まで) |
| Deep think | ×利用不可 | ×利用不可 | 〇利用可能(1日10回まで) |
Gemini Proの回数制限や画像・動画生成制限を見てみると、無料プランとProプランの差は非常に大きいのに対し、ProプランとUltraプランは使い方によっては無料プランとProプランほどの差は無いということが分かると思います。
各プランごとの機能的な違い

ここでは先ほどの表から具体的にはプランごとの機能や上限の違いとしてポイントになる部分を詳しく見ていきます!
①Gemini Proの回数制限
大きな違いとしてGemini Proモデルの回数制限があります。利用回数については以下の通りで、無料プランでもGemini Proを利用可能ですが、1日5回までという非常に低い回数制限が課せられています。無料プランではProモデルの利用はあくまでお試し程度と考えておきましょう。
| 無料プラン | Google AI Pro | Google AI Ultra | |
| Gemini Proの回数制限 | 1日5回まで | 1日100回まで | 1日500回まで |
業務などで常時質問するようなヘビーユーザーではない限りはほとんどの方にGoogle AI Proがおすすめです。
Gemini Flashモデルは速度重視ですが、複雑な指示を出すと回答が浅くなることがあります。一方、Gemini Proは「思考力」が格段に上がったモデルとなっており、特に以下のような質問をする方にはFlashではなくProモデルの使用をおすすめします!
Gemini Proモデルの使用が推奨されるタスク
- プログラミング: コードの生成、バグ修正、リファクタリング。
- 論理的推論: 複雑なデータ分析、数学的な問題解決、矛盾点の指摘。
- 長文ライティング: 構成案の作成、記事の執筆、論文の校正。
- 多言語翻訳: ニュアンスを汲み取った高精度な翻訳。
②画像生成・動画生成機能
次に各プランごとの画像生成機能と動画生成機能について詳しく見ていきましょう。
画像生成機能
画像生成機能は無料プランを含むすべてのプランで利用可能です。以下はプランごとの具体的な回数制限になります。
| 無料プラン | Google AI Pro | Google AI Ultra | |
| 画像生成機能 | 1日100枚まで利用可能 | 1日1000枚まで利用可能 | 1日1000枚まで利用可能 |
無料プランでも1日100枚まで生成可能なので画像生成だけに焦点を当てるのであれば、デザイン案を大量に出したいクリエイターなどではない限りは、まずは無料プランで使用するのがおすすめです。
動画生成機能
動画生成機能は無料プランでは利用できず、有料プランからとなっています。以下は動画生成機能のプランごとの制限になります。
| 無料プラン | Google AI Pro | Google AI Ultra | |
| 動画生成機能 | ×利用不可 | 〇1日3本まで利用可能 | 〇1日5本まで利用可能 |
無料プランでは動画生成が一切できませんが、Google AI Proであれば1日3本まで生成可能です。「たった3本?」と思われるかもしれませんが、プレゼン資料の導入動画や、SNS向けのショート動画の素材を作成する用途であれば、十分実用的な本数です。
また、別のGoogle Flowというサービスを利用するとさらに多くの動画を生成可能です!Pro/Ultraプラン契約者は、追加料金なしで利用でき、こちらは回数制限ではなくAIクレジットを使用して動画を生成するというシステムになっています。プランごとのAIクレジット付与数に関しては以下の通りです。
| 無料プラン | Google AI Pro | Google AI Ultra | |
| AIクレジット | 付与なし | 毎月1,000クレジット付与 | 毎月25,000クレジット付与 |
あくまで目安ですが、1つの動画を生成するのに20クレジット~となっています。Proプランの場合、Gemini上での動画生成上限はは1日3本までですが、付帯するAIクレジットを使ってGoogle Flow経由で生成すれば、さらに約50本(1000÷20)の生成が可能です!
1日に何十本も生成して試行錯誤したいというヘビーユーザーでない限り、月額36,400円のUltraプランを契約する必要性は薄いと言えます。
Google Flowについてさらに詳しく知りたい方は以下の記事を参照してください。
③Ultra限定機能
Proプランには搭載されていない機能として、自律的にタスクをこなす「Agent Mode」や、より深く思考する「Deep think」があります。
- Agent Mode:ユーザーに代わって複雑なタスクを自律的に実行する機能です。単に質問に答えるだけでなく、目標を達成するために、複数のステップに分解した計画を立て、ブラウザ操作などを行いながら自律的にタスクを実行・修正することが可能です。
- Deep think:Geminiの高度な推論モードです。並列思考技術を用いて、人間の思考のように複数の仮説を同時に検討し、より複雑な問題に対する深い思考と推論を行うことが可能です。
専門的な研究やハイレベルな要求を必要とする業務などで使用する場合にはこの2つの機能の利用を推奨します。
どちらもUltra(月額36,400円)専用の機能ですが、月額36,400円と非常に高額なため一般的なデスクワークやコンテンツ制作であれば、Proプランの機能で十分完結します。
Google AI Proを導入する5つのメリット
なぜ、最上位のUltraではなく、中間の「Google AI Pro」が多くの人に選ばれているのでしょうか。その理由を解説します。
①Gemini Proの圧倒的な推論能力
Gemini Proは、Flashと比較して「文脈理解」と「論理的推論」が飛躍的に向上しています。
- 数学などの論理的思考:大学レベルの高度な数学でも抜けの無い厳密な証明を提供してくれます。
- プログラミング:バグの特定だけでなく、「なぜそのエラーが起きたか」の解説と修正コードの提示がより的確になりました。
- マルチモーダル処理:画像や動画を読み込ませた際の認識精度が上がり、手書きのメモから正確な表データを作成するといった作業もスムーズに行えます。
ビジネスで「ミスの許されない資料作成」や学術的な「深い分析」を行うなら、FlashではなくProモデルが必須です。また、回数制限もほとんどの学生や社会人なら1日あたり100回まで利用可能なGoogle AI Proプランで十分です。
以下は具体例になります。ここではProモデルが得意な論理的な分析をテストします。状況設定は、
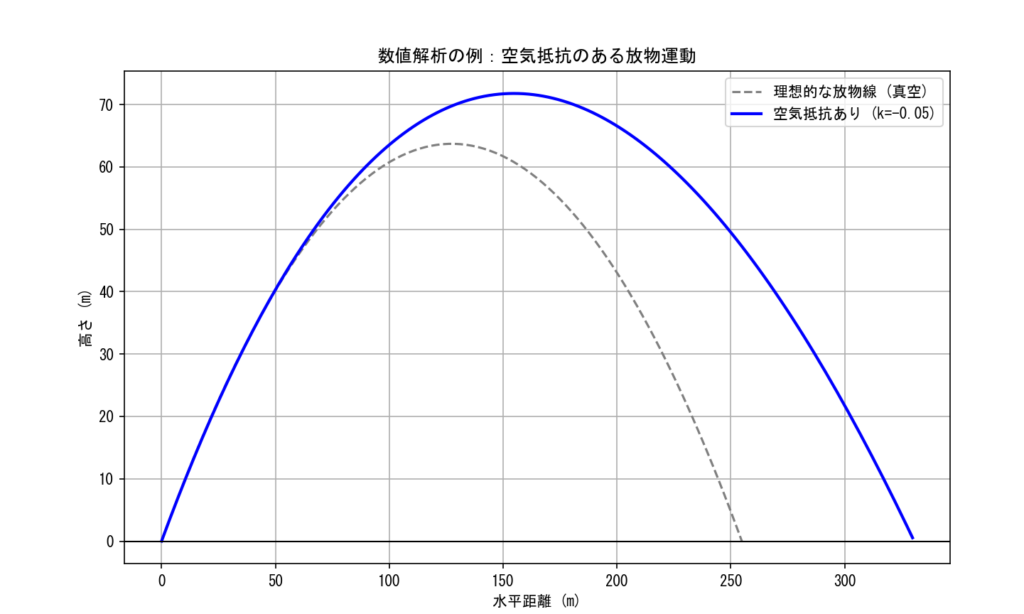
- 空気抵抗がある状態での放物運動と空気抵抗が無い状態(理想状態)での放物運動を観察するための数値解析をPythonで行う
- 出力された図がなぜか空気抵抗がある場合のほうが遠くへ飛んでいる
- どうしたら正しい結果になるのかをGeminiに聞き、生成されたプログラムコードをコピペして実行してみる
〇添付資料
# -*- coding: shift_jis -*-
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
def simulation():
# --- パラメータ設定 ---
g = 9.81 # 重力加速度 (m/s^2)
v0 = 50.0 # 初速度 (m/s)
angle = 45.0 # 打ち上げ角度 (度)
m = 1.0 # ボールの質量 (kg)
k = -0.05 # 空気抵抗係数(空気の粘り気のようなもの)
dt = 0.05 # 時間刻み (秒) - これを小さくするほど精度が上がる
# --- 初期状態の計算 ---
theta = np.radians(angle)
vx = v0 * np.cos(theta)
vy = v0 * np.sin(theta)
x = 0.0
y = 0.0
# 軌跡を保存するリスト
x_list = [x]
y_list = [y]
# --- 数値計算 (オイラー法) ---
# 地面に落ちる (y < 0) までループ
vx_curr, vy_curr = vx, vy
x_curr, y_curr = x, y
while y_curr >= 0:
# 1. 力を計算 (空気抵抗 F = -k * v と仮定)
# 加速度 a = F / m
ax = -(k / m) * vx_curr
ay = -g - (k / m) * vy_curr
# 2. 速度を更新 (v_new = v_old + a * dt)
vx_curr += ax * dt
vy_curr += ay * dt
# 3. 位置を更新 (x_new = x_old + v * dt)
x_curr += vx_curr * dt
y_curr += vy_curr * dt
# データを保存
if y_curr >= 0:
x_list.append(x_curr)
y_list.append(y_curr)
# --- 比較用:真空中の理論値 (高校物理の公式) ---
t_ideal = np.linspace(0, 2*v0*np.sin(theta)/g, 100)
x_ideal = v0 * np.cos(theta) * t_ideal
y_ideal = v0 * np.sin(theta) * t_ideal - 0.5 * g * t_ideal**2
# --- グラフ描画 ---
plt.figure(figsize=(10, 6))
plt.plot(x_ideal, y_ideal, label='理想的な放物線 (真空)', linestyle='--', color='gray')
plt.plot(x_list, y_list, label=f'空気抵抗あり (k={k})', color='blue', linewidth=2)
plt.title('数値解析の例:空気抵抗のある放物運動')
plt.xlabel('水平距離 (m)')
plt.ylabel('高さ (m)')
plt.axhline(0, color='black', linewidth=1) # 地面
plt.legend()
plt.grid(True)
plt.show()
if __name__ == "__main__":
simulation()〇プロンプト
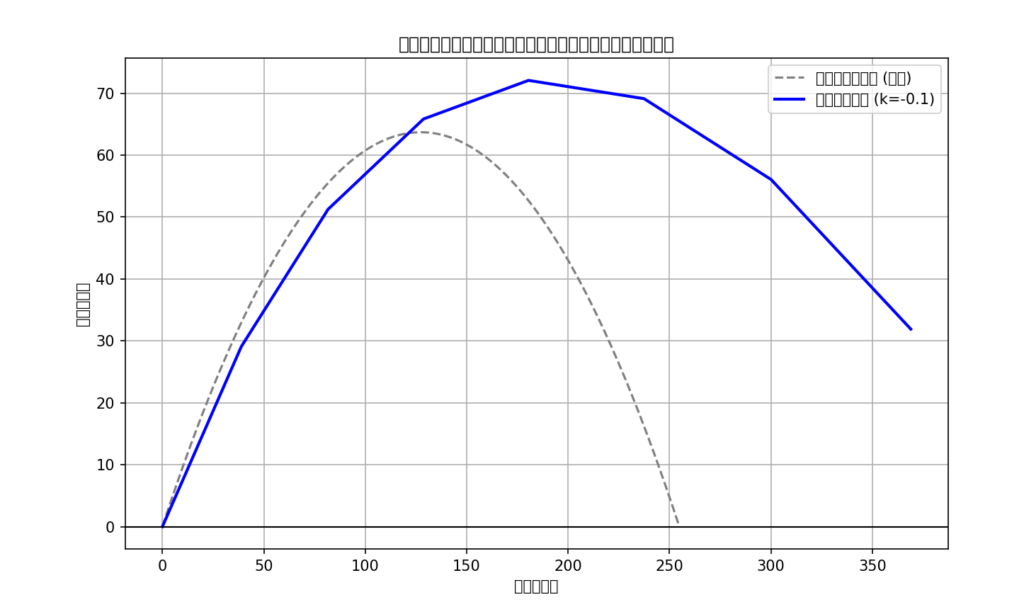
添付資料は空気抵抗がある状態での放物運動と空気抵抗が無い状態(理想状態)での放物運動を観察するためにPythonで数値解析を行った結果の図とコードです。添付図で、なぜか空気抵抗があるときのほうが遠くへ飛んでいます。どのような修正をすればよいですか?修正したフルコードをください。〇Gemini Flashの生成結果
# -*- coding: shift_jis -*-
import numpy as np
import matplotlib.pyplot as plt
def simulation_disaster():
# --- パラメータ設定 ---
g = 9.81 # 重力加速度
v0 = 50.0 # 初速度
angle = 45.0 # 打ち上げ角度
m = 1.0 # 質量
k = -0.1
dt = 1.0
# --- 初期状態の計算 ---
theta = np.radians(angle)
vx = v0 * np.cos(theta)
vy = v0 * np.sin(theta)
x = 0.0
y = 0.0
x_list = [x]
y_list = [y]
# --- 数値計算 (オイラー法) ---
vx_curr, vy_curr = vx, vy
x_curr, y_curr = x, y
while y_curr >= 0:
# 力を計算
ax = -(k / m) * vx_curr
ay = -g - (k / m) * vy_curr
# 速度を更新
vx_curr += ax * dt
vy_curr += ay * dt
# 位置を更新
x_curr += vx_curr * dt
y_curr += vy_curr * dt
if y_curr >= 0:
x_list.append(x_curr)
y_list.append(y_curr)
# --- 比較用:真空中の理論値 ---
t_ideal = np.linspace(0, 2*v0*np.sin(theta)/g, 100)
x_ideal = v0 * np.cos(theta) * t_ideal
y_ideal = v0 * np.sin(theta) * t_ideal - 0.5 * g * t_ideal**2
# --- グラフ描画 ---
plt.figure(figsize=(10, 6))
plt.plot(x_ideal, y_ideal, label='理想的な放物線 (真空)', linestyle='--', color='gray')
plt.plot(x_list, y_list, label=f'空気抵抗あり (k={k})', color='blue', linewidth=2)
plt.title('数値解析の例:空気抵抗がある放物運動')
plt.xlabel('横軸の距離')
plt.ylabel('縦軸の高さ')
plt.axhline(0, color='black', linewidth=1)
plt.legend()
plt.grid(True)
plt.show()
if __name__ == "__main__":
simulation_disaster()Gemini Flashではなぜか空気抵抗がある場合のほうが遠くへ飛んでいます、また図の文字部分も文字化けしてしまっています。
〇Gemini Proの生成結果
# -*- coding: shift_jis -*-
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
def simulation():
# --- パラメータ設定 ---
g = 9.81 # 重力加速度 (m/s^2)
v0 = 50.0 # 初速度 (m/s)
angle = 45.0 # 打ち上げ角度 (度)
m = 1.0 # ボールの質量 (kg)
k = 0.05 # 空気抵抗係数(空気の粘り気のようなもの)
dt = 0.05 # 時間刻み (秒) - これを小さくするほど精度が上がる
# --- 初期状態の計算 ---
theta = np.radians(angle)
vx = v0 * np.cos(theta)
vy = v0 * np.sin(theta)
x = 0.0
y = 0.0
# 軌跡を保存するリスト
x_list = [x]
y_list = [y]
# --- 数値計算 (オイラー法) ---
# 地面に落ちる (y < 0) までループ
vx_curr, vy_curr = vx, vy
x_curr, y_curr = x, y
while y_curr >= 0:
# 1. 力を計算 (空気抵抗 F = -k * v と仮定)
# 加速度 a = F / m
ax = -(k / m) * vx_curr
ay = -g - (k / m) * vy_curr
# 2. 速度を更新 (v_new = v_old + a * dt)
vx_curr += ax * dt
vy_curr += ay * dt
# 3. 位置を更新 (x_new = x_old + v * dt)
x_curr += vx_curr * dt
y_curr += vy_curr * dt
# データを保存
if y_curr >= 0:
x_list.append(x_curr)
y_list.append(y_curr)
# --- 比較用:真空中の理論値 (高校物理の公式) ---
t_ideal = np.linspace(0, 2*v0*np.sin(theta)/g, 100)
x_ideal = v0 * np.cos(theta) * t_ideal
y_ideal = v0 * np.sin(theta) * t_ideal - 0.5 * g * t_ideal**2
# --- グラフ描画 ---
plt.figure(figsize=(10, 6))
plt.plot(x_ideal, y_ideal, label='理想的な放物線 (真空)', linestyle='--', color='gray')
plt.plot(x_list, y_list, label=f'空気抵抗あり (k={k})', color='blue', linewidth=2)
plt.title('数値解析の例:空気抵抗のある放物運動')
plt.xlabel('水平距離 (m)')
plt.ylabel('高さ (m)')
plt.axhline(0, color='black', linewidth=1) # 地面
plt.legend()
plt.grid(True)
plt.show()
if __name__ == "__main__":
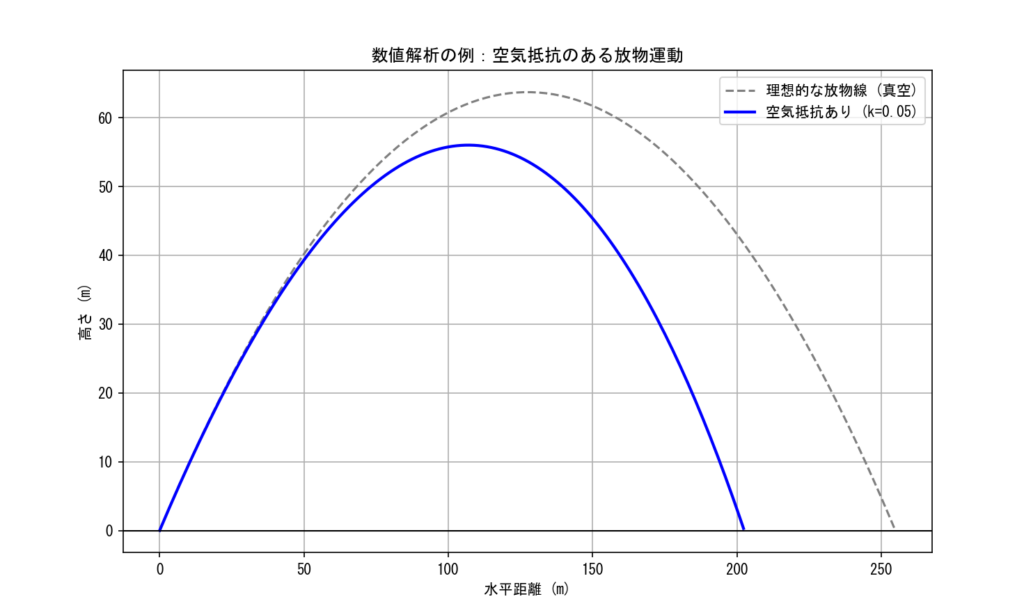
simulation()Gemini Proでは図を見てわかる通り、正しく修正することができました。
実際、Gemini Flashはいじる必要のない箇所を修正してしまい、さらに結果が悪くなっていました。Gemini Proでは添付画像の図の形状を理解し、「なぜこの形状なのか?」を考えて、最終的にパラメータ調整を行うことにより正しい修正ができていました。
②2TBのクラウドストレージが付属
Google AI Proは、2TBのクラウドストレージもセットになっているため、別途Google Oneでストレージを契約しているユーザーにとっては、実質的な追加コストを抑えてAIを導入できます。
2TBのGoogle One(クラウドストレージ)プランの料金が月額1,300円なので実質1,600円でGoogleのAIを導入できる計算になります!「性能」と「価格」のバランスが最も優れているのがこのプランです。
③Google Workspaceとのシームレスな連携
ビジネス利用において最も恩恵を感じやすいのが、Google Workspaceアプリ(Docs, Gmail, Drive, Slides, Sheets)内でのAI連携です。
無料版では「Geminiのチャット画面で文章を作り、それをコピーしてドキュメントに貼り付ける」という作業が必要でしたが、Google AI Proプランの方なら、アプリ内で直接AIを呼び出せます。具体的には以下のような使い方ができます!
- Gmail: 受信メールを開いたまま「このメールへの返信案を丁寧に作成して」と指示出しが可能。
- Googleドキュメント: 執筆中に「この段落をもっとフォーマルに書き直して」「続きの構成案を出して」とシームレスに編集。
- Googleスライド: テキストのプロンプトから、プレゼン資料のデザインと構成を一発で生成。
アプリを行き来する「スイッチングコスト」をゼロにし、業務スピードを物理的に加速させることができるのが、Google AI Proを選ぶ非常に大きなメリットです。
具体的には以下のようなことが可能です。今回はGoogleドキュメントの「改良」機能を使ってみます。今回はあえて、学生が書いたような校正が必要そうな文章をつかい、よりフォーマルな文章にしてみます。
〇元の文章
円安っていうのは、円の価値が他の国の通貨、例えばアメリカのドルとかと比べて安くなるってことです。これはすごく大事な経済の話です。
円安になると、1ドルを交換するときに前よりも多くの日本円が必要になるってことになります。例えば、前は1ドルが100円だったのに、円安になると1ドルが150円になる、みたいな感じです。100円で買えてたものが150円出さないと買えなくなるから、円の力が弱くなっているっていう意味です。〇Geminiの改良後(よりフォーマルに)
円安とは、日本円の価値が、外国の通貨、例えばアメリカドルなどと比較して相対的に下落する経済現象を指します。これは、経済において非常に重要な意味を持ちます。
円安が進行すると、1米ドルを交換するために必要となる日本円の金額が増加します。具体的には、以前は1ドルが100円であったものが、円安により1ドルが150円になる、といった状況です。これは、従来100円で購入できたものが150円を支払わなければ購入できなくなることを意味し、日本円の購買力が低下していることを示します。
このように「改良」機能を使うと元の文章の内容はそのままに、しっかりとした言葉遣いや文章校正で書き換えてくれます!
④Google Flowが追加コストなしで利用可能
Google AI Proユーザーの大きな特権として、最新のAI動画生成ツール「Google Flow」を利用できる点が挙げられます。
先ほども動画生成の箇所で説明した通り、Google AI Proならプラン内に毎月付与されるAIクレジットを使用することで、追加コストなしでAI動画生成、編集を始められます。
動画制作を外注したり、高額な専用ツールを契約したりするコストを考えれば、この機能だけで月額料金の元が取れると言っても過言ではありません。
具体的な活用法としては、商品紹介のイメージ動画を生成するなどがあります。
〇プロンプト
商品紹介用の動画素材を作りたいです。添付画像の60系プリウスの360°回転動画を生成してください。


〇生成結果
このように、動画生成時の画像添付機能を使いイメージ通りの紹介動画を生成することが可能です!
⑤NotebookLMの機能が拡張
Googleが提供する大注目のリサーチ・学習ツール「NotebookLM」においても、Google AI Proユーザーは拡張された機能を利用できます。
NotebookLMは、手持ちのPDF資料やWebサイトのURLを読み込ませることで、その資料に基づいた回答をしてくれる「RAG(検索拡張生成)」ツールですが、Proプランでは「NotebookLM Plus」という上位版を利用できます!
具体的には以下のように回数制限が緩和されます。
| NotebookLM(通常版) | NotebookLM Plus | |
| 1日あたりの質問回数 | 50回まで | 500回まで |
| 1日あたりの音声要約生成数 | 3回まで | 20回まで |
| ノートブック数 | 100件まで | 500件まで |
| ソース数 | 50件まで | 300件まで |
大量の資料を読み込む必要がある研究者や、社内マニュアルを学習させたいビジネスパーソンにとって、この拡張機能は強力な武器となります。
具体的には以下のような使い方ができます。今回は架空の社内オリエンテーションマニュアルを作り、アップロードしました。
〇プロンプト
新入社員をサポートする主要部署と、社内交流を促進する具体的な仕組みは何ですか?〇生成結果
新入社員をサポートする主要部署と、社内交流を促進する具体的な仕組みについて、提供された資料に基づいてご説明します。
### I. 新入社員をサポートする主要部署
新入社員のサポート、手続き、オリエンテーションなどを主に担当するのは、**人事部**と**総務部**です。
1. **人事部**
人事部は、新入社員が円滑に勤務をスタートするための基本的な情報提供や手続きを主に担当します。
* **オリエンテーションでの担当内容**: 開会の挨拶、会社概要の説明、就業規則・服務規程の説明、各種申請手続き、福利厚生に関する説明を行います。
* **困りごとの連絡先**: 業務や社内のことで不明点や困りごとがある場合の連絡先として、**採用、給与、休暇**に関する窓口となります。
* **所在地**: 人事部はオフィスビルの3階に位置し、各種手続きの窓口となっています。
2. **総務部**
総務部は、主に会社の環境やインフラに関するサポートを担当します。
* **オリエンテーションでの担当内容**: IT環境、情報セキュリティに関する説明を担当します。また、**職場案内**や**部署紹介**も総務部が担当します。
* **困りごとの連絡先**: 以下の項目について連絡窓口となります。
* **PC・システム関連**(総務部 IT担当)
* **備品・施設関連**(総務部)
### II. 社内交流を促進する具体的な仕組み
資料に記載されている、社内交流を促進するための具体的な仕組みは、主に以下の二つです。
1. **ランチ交流会**
* **目的**: 新入社員を歓迎するため。
* **内容**: **配属部署のメンバー**とのランチ交流会が開催されます。
* **時期**: **配属後1週間以内**に開催され、詳細は部署責任者より案内があります。
2. **全社キックオフミーティング**
* **目的**: 全社員が集まり、**業績報告と次期の目標を共有**するため。
* **頻度**: **半期に一度**実施されます。
これらの仕組みは、新入社員が当社の文化や働き方を理解し、一日でも早く会社に慣れることの一助となることが期待されています。このように知りたい箇所のみを分かりやすくまとめ直してくれます!
最適なプランの選び方まとめ
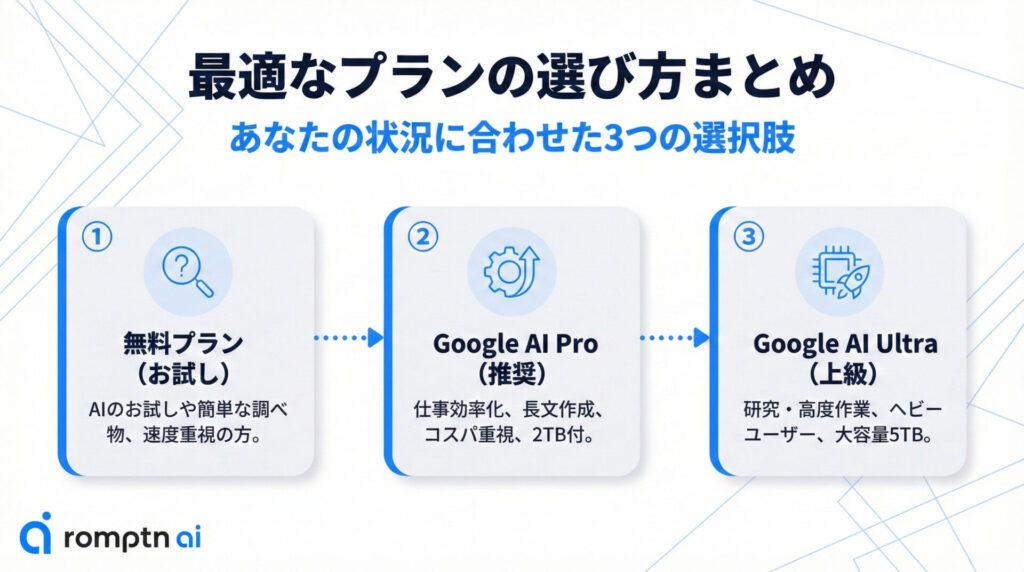
最後に、あなたの状況に合わせた最適なプランの選び方をまとめます。
無料プランがおすすめな人
- AIをまずは無料で試してみたい人
- 簡単なメールの返信作成や、日常の調べ物に使いたい人
- 回答の「精度」よりも「速度」を重視する人
無料プランはGeminiの最低限の機能を利用することができます。日常のちょっとした調べ物などに使いたい方や、Google AI Proプランを契約するか迷っている方はまずはこの無料プランから試してみてください!
Google AI Proがおすすめな人
- 仕事で本格的にAIを活用して効率化したい人
- 長文の要約、記事作成、複雑なデータ分析を行いたい人
- GoogleドキュメントやGmailでのAI連携機能を使いたい人
- 最もコストパフォーマンス良く高性能AIを使いたい人
- 2TBのストレージも合わせて確保したい人
Google AI Proは一番スタンダードなプランとなっています。また、GoogleのAI関係のほとんどの機能を利用可能で、各種回数制限も十分実用的な範囲で設定されています。2TBのクラウドストレージがついてくるという点も非常に大きなポイントになっています。
Google AI Ultraがおすすめな人
- 1日に数百回以上AIと対話するヘビーユーザー
- 研究や業務で高度な作業に使用する場合
- 開発業務などでAPI制限や回数制限を気にしたくない人
- 動画編集などを行い、5TB以上の大容量ストレージが必要なクリエイター
- 常に最高速の環境でストレスなく作業したい人
Google AI Ultraは主に研究や業務で高度な作業に使用する場合に適したプランです。Ultraプラン限定機能の「Agent Mode」や「Deep think」機能があったり、非常に高く設定された回数制限などがありますが、一般的なユーザーではそのほとんどを持て余してしまいます。
Ultraプランは本来は企業や開発チームが導入するレベルのスペックを個人開放しているため他のプランに比べて月額36,400円と非常に高額になっています。
個人ユーザーはいきなりGoogle AI Ultraにする前に、Google AI Proプランを契約してみてどうしても不満があればGoogle AI Ultraプランを契約する流れがおすすめです。
まとめ:Google AI Proはコスパ最強
この記事では、新しくなったGoogleのAIプラン体系について、無料プラン・Google AI Pro・Google AI Ultraの違いを徹底解説しました。
プラン選びで迷った際に最も重要なのは、「コストに対してどれだけのパフォーマンス(時短・効率化)が得られるか」です。その観点で言えば、Google AI Proは間違いなく最もコストパフォーマンスに優れた選択肢と言えます。
この記事のポイントをまとめると以下の通りです。
- Google AI Proがほとんどのユーザーの最適解:Gemini Proを1日100回使えて、動画生成やWorkspace連携も付帯する「コスパ最強」のプラン。
- 無料版はあくまで「お試し」:Gemini Proの利用が1日5回に限られるため、本格的な業務利用には不向き。
- Ultraはプロフェッショナル専用:月額36,400円と高額。「Agent Mode」などが必要な特殊な業務・研究用途以外ではオーバースペックになる可能性が高い。
- 2TBストレージの恩恵:Google AI Proにはストレージ特典が含まれるため、実質的なAIコストはさらに安く感じられる。
もし現在、無料プランを使用していて「もう少し賢い回答が欲しい」「制限を気にせず使い倒したい」と感じているなら、まずはGoogle AI Proを試してみてください!

















