最近Googleから「Gemini 3.0」、OpenAIから「ChatGPT 5.1」が発表され、それぞれ高性能なAIとして注目を集めています。
最新のAIの動向に敏感なあなたにとって、「結局、どっちのAIが優れているの?」「どちらを使うべきなの?」という疑問は尽きないはずです。
そこで本記事では、最新の情報をベンチマークの数値や、実際に両者に同じプロンプトを入力した検証結果に基づき、Gemini 3.0とChatGPT 5.1を7つの項目で徹底的に比較します。
この記事を読めば、両者の数値的な差、料金体系、そしてどちらを使うべきかが客観的にわかります。Gemini3.0とChatGPT5.1の具体的な違いを分かりやすく解説していきますので、ぜひ最後までご覧ください。
内容をまとめると…
Gemini3.0とChatGPT5.1は史上最高レベルのモデル。
各種ベンチマークで、Gemini3.0がChatGPT5.1を圧倒
特にマルチモーダル(視覚)に関してGeminiはずば抜けている
どちらも無料プランで使うことができるが、制限が設けられている
高性能すぎて普段の作業では困らないほどの出来
豪華大量特典無料配布中!
romptn aiが提携する完全無料のAI副業セミナーでは収入UPを目指すための生成AI活用スキルを学ぶことができます。
ただ知識を深めるだけでなく、実際にAIを活用して稼いでいる人から、しっかりと収入に直結させるためのAIスキルを学ぶことができます。
現在、20万人以上の人が収入UPを目指すための実践的な生成AI活用スキルを身に付けて、100万円以上の収益を達成している人も続出しています。
\ 期間限定の無料豪華申込特典付き! /
AI副業セミナーをみてみる











Gemini3.0とChatGPT5.1の特徴を整理
まずは、Googleの「Gemini3.0」とOpenAIの「ChatGPT 5.1」という、同時期にリリースされた2大AIモデルの特徴をそれぞれ整理しましょう。
Gemini3.0の特徴
Googleによって開発された「Gemini」は、2025年11月に正式発表された最新の生成AIモデルで、従来のシリーズを大きく進化させた、Googleが「史上最高のAIモデル」と公式で評価するモデルです。
特に、大規模な情報処理能力と多様なデータの理解に優れており、Google CEOのスンダー・ピチャイ氏が「これまでで最も科学的であり、あらゆるアイデアを実現するモデル」と豪語するほどの衝撃を開発者界隈に与えています。
Gemini 3.0の主な進化ポイントを以下にまとめます。
| 進化ポイント | 詳細(従来モデルからの改善点) |
|---|---|
| 推論能力の強化 | 複雑な問題への対応力向上、意図・文脈理解力が世界最高水準に達した。 |
| 真のマルチモーダル | テキスト、画像、音声、動画、コードに3Dデータなどを加えた多様な情報ソースを統合して処理・生成可能。 |
| 超長文コンテキスト | 1Mトークンのコンテキストウィンドウに対応。長いプログラムやドキュメントの生成・リファクタリングを効率よく行える。 |
| 自動化(エージェント) | 複雑なタスクを自動遂行するGemini Agent(ジェミニエージェント)が搭載された。 |
| 高度な推論モード | 高度な問題解決を可能にする「Deep Thinkモード」を提供。 |
| 広範な展開 | Google検索(AIモード)やAI Studioなど、多くのGoogle製品へ順次展開。 |
※それぞれの機能は順次展開とされているため利用環境によっては利用不可。
Gemini3.0についてSNSでは以下のような満足・驚きの声が多数投稿されています。
特に、「簡単にアプリが作れる!」などの開発環境での使いやすさや性能に驚く声が多かったです。
ChatGPT5.1の特徴
OpenAIが開発した「ChatGPT」は、その登場以来、自然な対話能力と多様なタスク処理能力で業界をリードしてきました。ChatGPT 5.1は2025年11月にリリースされたGPT-5の改良版であり、単なる性能向上だけでなく、ユーザー体験を根本から見直した大幅なアップデートです 。
賢さだけでなく「会話が楽しい」ことを重視し、より温かく会話的な応答が特徴です 。ChatGPT 5.1の主な進化ポイントを以下にまとめます。特に、構造化された応答の精度と推論能力の強化に焦点が当てられています 。
| 進化ポイント | 詳細(GPT-5からの改良点) |
| Instant / Thinkingモード | Instantモードは即時応答・会話のしやすさに優れ、Thinkingモードは複雑な推論に特化 。必要に応じて考える時間を自動調整(適応的推論)しつつ高速応答を実現 。 |
| 指示追従性の大幅改善 | ユーザーの文字数や形式など細かい指示をより正確に実行可能に。作業の自動化や業務利用が容易になった 。 |
| パーソナライズ機能 | 会話のトーンを「プロフェッショナル」「皮肉っぽい」など8種類のスタイルから選択可能。長い対話の文脈保持も強化され、一貫性が向上。 |
| 信頼性と安全性の向上 | 誤答や虚偽表現が大幅に減少。Thinkingモードでは以前のモデルより80%もミスが少なくなっている。感情的・精神的に不安定な方への対応精度も向上。 |
| パフォーマンス最適化 | より少ないトークンで高品質な出力を実現し、API利用効率の向上や応答速度の改善を実現。ワークフローに適している。 |
特に、回答生成の際にタスクの難易度に応じて回答生成時間(思考の深さ)を適切に選択することによって、より満足できる回答が生成できるようなったのが特徴です。
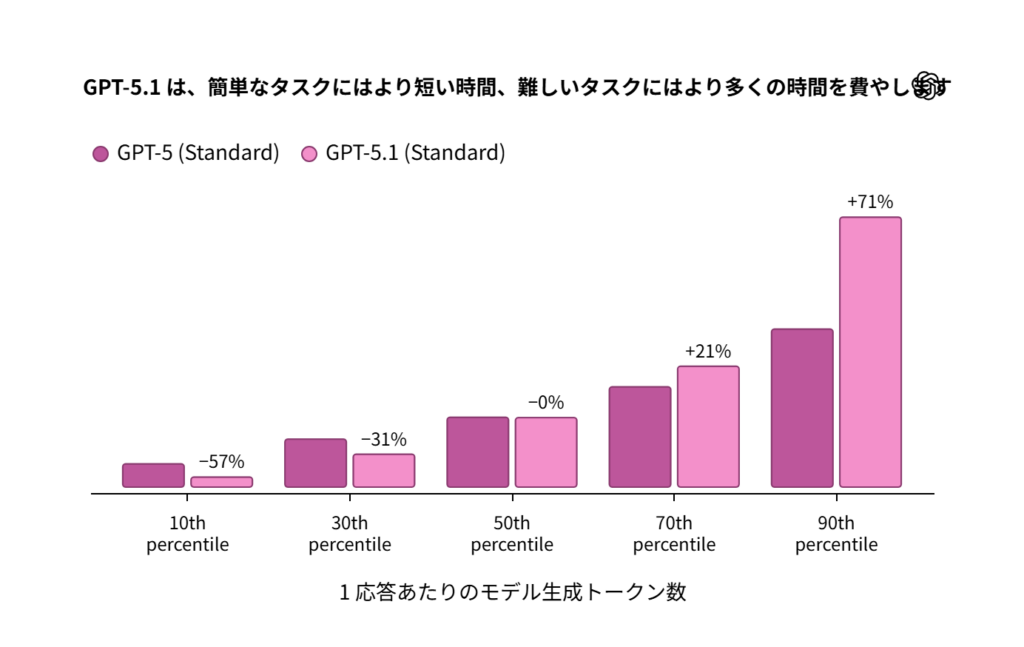
ChatGPT5.1に関して、Xでは以下のような肯定的なポストが多く投稿されていました。
前回のChatGPT5.0よりも、指示に対する回答の正確さと会話の速度と精度のバランスがよくなったという意見が多かったです。
ベンチマークで性能を比較
ここからは、そんな高性能なGemini3.0とChatGPT5.1をベンチマークの数値をもとに客観的に両者の性能を比較したいと思います。
以下はGoogle公式から発表されたGeminiの各モデルとChatGPTを比較したベンチマークの結果です。
| ベンチマーク | 説明 | Gemini 3 Pro | Gemini 2.5 Pro | GPT-5.1 |
| Humanity’s Last Exam | 学術的な推論 | 37.5% (ツールなし) 45.8% (コードと検索あり) | 21.6% | 26.5% |
| ARC-AGI-2 | 視覚的なパズル推論 | 31.1% | 4.9% | 17.6% |
| GPQA Diamond | 科学的な知識 | 91.9% | 86.4% | 88.1% |
| AIME 2025 | 数学 | 95.0% (ツールなし) 100% (コード実行あり) | 88.0% | 94.0% |
| MathArena Expert | 困難な数学コンテスト問題 | 23.4% | 0.5% | 1.0% |
| MMMU-Pro | マルチモーダルな理解と推論 | 81.0% | 68.0% | 76.0% |
| ScreenSpot-Pro | スクリーン理解 | 72.7% | 11.4% | 3.5% |
| CharXiv Reasoning | 図表からの情報抽出 | 81.4% | 69.6% | 69.5% |
| OmniDocBench 1.5 | OCR(光学文字認識) | 0.115 (全体エディット距離、低い方が良い) | 0.145 | 0.147 |
| Video-MMMU | 動画からの知識獲得 | 87.6% | 83.6% | 80.4% |
| LiveCodeBench Pro | 競技プログラミングの問題(コード、推論、IOIから) | 2,439 (Eloレーティング、高い方が良い) | 1,775 | 2,243 |
| Terminal-Bench 2.0 | エージェント的なターミナル制御 | 54.2% | 32.6% | 47.6% |
| SWE-Bench Verified | エージェント的なコーディング | 76.2% (シングルアテンプト) | 59.6% | 76.3% |
| t2-bench | エージェント的なツール使用 | 85.4% | 54.9% | 80.2% |
| Vending-Bench 2 | 長期的なエージェントタスク | $5,478.16 (純資産(平均)、高い方が良い) | $573.64 | $1,473.43 |
| FACTS Benchmark Suite | 内部グラウンディング、パラメトリック、MM、検索ベンチマークを統合 | 70.5% | 63.4% | 50.8% |
| SimpleQA Verified | パラメトリック知識 | 72.1% | 54.5% | 34.9% |
| MMMLU | 多言語のQ&A | 91.8% | 89.5% | 91.0% |
| Global PIQA | 文化と国境を越えた一般的な推論 | 93.4% | 91.5% | 90.9% |
| MRCR v2 (8-needle) | 長いコンテキストの理解 | 77.0% (128Kコンテキスト) 26.3% (1Mコンテキスト) | 58.0% 16.4% | 61.6% (非サポート) |
評価方法の詳細
太字になっている個所が各ベンチマークにおける最高スコアです。
数値的に見るとGemini3.0が圧倒的ですね。
Gemini 3 Proは、特に推論、マルチモーダル(視覚)の分野において、ChatGPT 5.1を大きく凌駕しています 。
ChatGPT 5.1は、SWE-Bench Verified(エージェント的なコーディング)など一部のベンチマークでGemini 3 Proと拮抗していますが 、全体的なバランスでは、Geminiに優位性が見られます。
Gemini3.0とChatGPT5.1の性能を7つの項目で比較
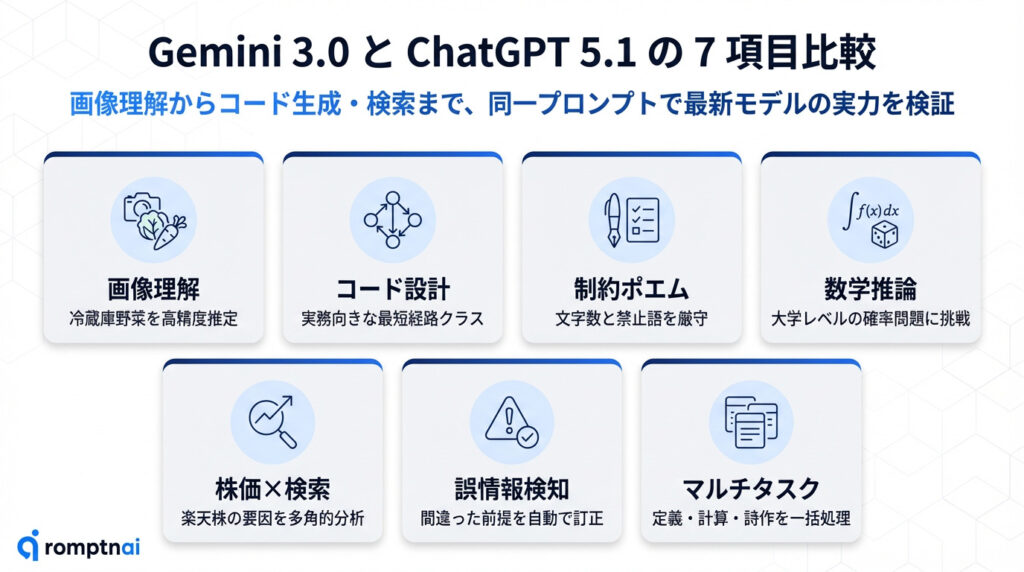
ここでは、両者に同じプロンプトを投げて「一発勝負」で7つのタスクを比較します。先に結果だけお伝えすると、7項目中4項目でGemini 3.0、3項目でChatGPT 5.1が優勢という僅差の勝負になりました。それぞれの項目で、どのような違いが出たのかを順に見ていきましょう。
| 対決項目 | Gemini3.0 | ChatGPT5.1 |
|---|---|---|
| 画像の解釈 | 〇 | |
| 複雑なコーディング | 〇 | |
| 制約付きの創作活動(指示の順守) | 〇 | |
| 数学的推論 | 〇 | |
| リアルタイムの情報検索と推論 | 〇 | |
| ハルシネーション(嘘)の自己検出と訂正 | 〇 | |
| 複数タスクの同時処理 | 〇 | |
| 最終結果 | 4 | 3 |
画像の解釈 (Gemini3.0の勝利)
まずは、画像における空間把握能力と判断力を競ってもらいましょう。以下の写真とプロンプトをもとに、冷蔵庫の中の野菜をできるだけリストアップしてもらい、その精度を比較します。

冷蔵庫の中にある食材をリストアップしてください。
見えている食材の奥の方にある見えにくい食材もできる限り特定してください。
Gemini3.0

ChatGPT5.1

どちらも隠れた部分の野菜までしっかり推測・判断してリストにしてくれました。しかし、認識した数は同じくらいですが、判断の精度に差が現れました。
Geminiが、香草類(おそらくパクチー)やズッキーニ、サニーレタスを正確に識別できているのに対し、ChatGPTは香草類をほうれん草、ズッキーニをきゅうり、サニーレタスを単なるレタスと誤認しています。
ChatGPTは、冷蔵庫奥の葉物の下に見える長ネギのような白い茎を認識できているという点ではGeminiに勝っていますが、全体的な正確性を見るとこの対決は「Gemini3.0」の勝利です。
複雑なコーディング (ChatGPT5.1の勝利)
生成AIを使う上でコーディングの能力は非常に重要です。ここでは以下のプロンプトを使用してコーディングの正確さと設計の効率性を見ていきましょう。
Visual Studioで実行できるようにPythonでコードを書いてください。
加重付き有向グラフを表すクラスを設計し、そのクラスにダイクストラ法を実装してください。
この実装では、特定の始点から他のすべてのノードへの最短経路とそのコストを求められるようにしてください。
ノードの追加・削除、エッジの追加・削除のメソッドも含めてください。
また、実装段階で工夫した点もコードの中に記述してください。Gemini3.0
import heapq
import sys
class WeightedDirectedGraph:
"""
加重付き有向グラフを表すクラス
ダイクストラ法による最短経路探索をサポート
"""
def __init__(self):
# 隣接リストとして辞書を使用
# 構造: {node_id: {neighbor_id: weight, ...}, ...}
self.adj_list = {}
def add_node(self, node):
"""
ノードを追加する
既に存在する場合は何もしない
"""
if node not in self.adj_list:
self.adj_list[node] = {}
def add_edge(self, u, v, weight):
"""
エッジを追加する (u -> v)
ノードが存在しない場合は自動的に作成する
"""
# [工夫点] 負の重みはダイクストラ法で扱えないため、事前にエラーを出して防ぐ
if weight < 0:
raise ValueError("Dijkstra's algorithm does not support negative weights.")
self.add_node(u)
self.add_node(v)
self.adj_list[u][v] = weight
def remove_node(self, node):
"""
ノードを削除する
そのノードに関連するエッジも全て削除する
"""
if node in self.adj_list:
# 1. ノード自体(およびそこから出るエッジ)を削除
del self.adj_list[node]
# 2. 他のノードからこのノードへ向かうエッジを削除
# [工夫点] 全ノードを走査するためコストがかかるが、整合性を保つために必須
for u in self.adj_list:
if node in self.adj_list[u]:
del self.adj_list[u][node]
def remove_edge(self, u, v):
"""
エッジを削除する (u -> v)
"""
if u in self.adj_list and v in self.adj_list[u]:
del self.adj_list[u][v]
def dijkstra(self, start_node):
"""
ダイクストラ法を用いて、始点から全ノードへの最短経路とコストを求める
Returns:
distances (dict): 各ノードへの最小コスト
path_info (dict): 経路復元用の情報 (node -> prev_node)
"""
if start_node not in self.adj_list:
return None, None
# 初期化
# [工夫点] Pythonでは無限大を float('inf') で表現可能
distances = {node: float('inf') for node in self.adj_list}
distances[start_node] = 0
# 経路復元用のマップ (curr -> prev)
previous_nodes = {node: None for node in self.adj_list}
# 優先度付きキュー (cost, node)
# [工夫点] heapqを使うことで、常に最小コストのノードを O(log V) で取り出せる
priority_queue = [(0, start_node)]
while priority_queue:
current_cost, current_node = heapq.heappop(priority_queue)
# [工夫点] 遅延削除 (Lazy Deletion) の対応
# キューに同じノードの古い情報(高コスト)が残っている場合があるため、
# 確定済みの最短距離よりコストが大きい場合はスキップする
if current_cost > distances[current_node]:
continue
# 隣接ノードを確認
for neighbor, weight in self.adj_list[current_node].items():
distance = current_cost + weight
# より短い経路が見つかった場合のみ更新
if distance < distances[neighbor]:
distances[neighbor] = distance
previous_nodes[neighbor] = current_node
heapq.heappush(priority_queue, (distance, neighbor))
return distances, previous_nodes
def get_shortest_path(self, start_node, target_node):
"""
ダイクストラ法の結果を利用して、具体的な経路リストを返す
"""
distances, previous_nodes = self.dijkstra(start_node)
if distances is None or distances[target_node] == float('inf'):
return [], float('inf')
path = []
curr = target_node
while curr is not None:
path.append(curr)
curr = previous_nodes[curr]
# ゴールから遡っているので反転させる
return path[::-1], distances[target_node]
# --- 実行確認用コード ---
if __name__ == "__main__":
# グラフのインスタンス作成
g = WeightedDirectedGraph()
# エッジの追加 (ノードは自動追加)
print("--- グラフの構築 ---")
g.add_edge('A', 'B', 1)
g.add_edge('A', 'C', 4)
g.add_edge('B', 'C', 2)
g.add_edge('B', 'D', 5)
g.add_edge('C', 'D', 1)
# 現時点の最短経路
print("\n--- 'A' からの最短経路 (初期状態) ---")
dists, _ = g.dijkstra('A')
for node, cost in dists.items():
print(f"To {node}: Cost {cost}")
# 経路復元のテスト
path, cost = g.get_shortest_path('A', 'D')
print(f"\nPath A -> D: {path} (Cost: {cost})")
# A -> B(1) -> C(2) -> D(1) = Total 4
# 動的な変更: エッジの削除
print("\n--- エッジ B->C を削除 ---")
g.remove_edge('B', 'C')
path, cost = g.get_shortest_path('A', 'D')
print(f"Path A -> D: {path} (Cost: {cost})")
# B->Cがなくなったので、A->B->D(Cost 1+5=6) または A->C->D(Cost 4+1=5) になるはず
# 動的な変更: ノードの追加とエッジ接続
print("\n--- ノード E を追加し、C->E, E->D を接続 ---")
g.add_edge('C', 'E', 1)
g.add_edge('E', 'D', 1) # C->D(1) より C->E->D(2) は遠いが、もしC->Dを消せば効いてくる
path, cost = g.get_shortest_path('A', 'E')
print(f"Path A -> E: {path} (Cost: {cost})")
# 動的な変更: ノードの削除
print("\n--- ノード C を削除 ---")
g.remove_node('C')
dists, _ = g.dijkstra('A')
print("Costs from A after deleting C:")
for node, cost in dists.items():
print(f"To {node}: Cost {cost}")実行結果

ChatGPT5.1
from __future__ import annotations
from typing import Dict, Hashable, List, Tuple, Any
import heapq
import math
class DirectedWeightedGraph:
"""
加重付き有向グラフを表すクラス。
ノードはハッシュ可能なオブジェクト(int, str など)であればOK。
内部表現は
adjacency[u][v] = weight
という dict of dict を使う。
"""
def __init__(self) -> None:
# 工夫1: 隣接リストを dict-of-dict で管理
# - adjacency[u] = {v1: w1, v2: w2, ...}
# - エッジ追加・削除が O(1) に近い形で扱いやすい
self.adjacency: Dict[Hashable, Dict[Hashable, float]] = {}
# ========== ノード操作メソッド ==========
def add_node(self, node: Hashable) -> None:
"""ノードを追加する(既に存在する場合は何もしない)"""
if node not in self.adjacency:
self.adjacency[node] = {}
def remove_node(self, node: Hashable) -> None:
"""
ノードを削除する。
・そのノードから出るエッジ
・そのノードへ向かうエッジ
の両方を削除する。
"""
if node not in self.adjacency:
return
# 工夫2: 「そのノードへのエッジ」もまとめて削除
for u in list(self.adjacency.keys()):
if node in self.adjacency[u]:
del self.adjacency[u][node]
# ノード自体を削除
del self.adjacency[node]
# ========== エッジ操作メソッド ==========
def add_edge(self, u: Hashable, v: Hashable, weight: float) -> None:
"""
有向エッジ u -> v を追加する。
weight は 0 以上を想定(ダイクストラ法前提)。
"""
if weight < 0:
raise ValueError("ダイクストラ法では負の重みは扱えません。")
# 工夫3: ノードが存在しなければ自動的に追加
self.add_node(u)
self.add_node(v)
self.adjacency[u][v] = float(weight)
def remove_edge(self, u: Hashable, v: Hashable) -> None:
"""エッジ u -> v を削除する(存在しない場合は何もしない)"""
if u in self.adjacency and v in self.adjacency[u]:
del self.adjacency[u][v]
# ========== ダイクストラ法 ==========
def dijkstra(self, start: Hashable) -> Tuple[Dict[Hashable, float], Dict[Hashable, Any]]:
"""
ダイクストラ法で start から各ノードへの最短距離を計算する。
戻り値:
dist: 各ノードまでの最短距離 (到達不能な場合は math.inf)
prev: 最短経路における直前ノード(start の prev[start] は None)
"""
if start not in self.adjacency:
raise ValueError(f"始点ノード {start!r} はグラフ内に存在しません。")
# 初期化
dist: Dict[Hashable, float] = {node: math.inf for node in self.adjacency}
prev: Dict[Hashable, Any] = {node: None for node in self.adjacency}
dist[start] = 0.0
# 優先度付きキュー (距離, ノード)
# 工夫4: 「遅延更新(lazy)」戦略を採用
pq: List[Tuple[float, Hashable]] = []
heapq.heappush(pq, (0.0, start))
while pq:
cur_dist, u = heapq.heappop(pq)
# すでにより短い距離が見つかっている場合はスキップ
if cur_dist > dist[u]:
continue
# 隣接ノードを緩和
for v, w in self.adjacency[u].items():
new_dist = dist[u] + w
if new_dist < dist[v]:
dist[v] = new_dist
prev[v] = u
heapq.heappush(pq, (new_dist, v))
return dist, prev
def reconstruct_path(self, start: Hashable, goal: Hashable,
prev: Dict[Hashable, Any]) -> List[Hashable]:
"""
dijkstra の結果得られた prev を用いて、start から goal までの経路を復元する。
到達不能な場合は空リストを返す。
"""
if prev.get(goal, None) is None and start != goal:
# start 自身以外で、prev が None の場合は到達不能
return []
path: List[Hashable] = []
cur = goal
while cur is not None:
path.append(cur)
cur = prev[cur]
path.reverse()
if path and path[0] == start:
return path
else:
return []
def shortest_paths_from(self, start: Hashable) -> Tuple[Dict[Hashable, float], Dict[Hashable, List[Hashable]]]:
"""
始点 start から全ノードへの
・最短距離
・具体的な経路(ノード列)
をまとめて返すヘルパーメソッド。
"""
dist, prev = self.dijkstra(start)
# 工夫5: 各ノードへの「経路」も同時に辞書で返す
paths: Dict[Hashable, List[Hashable]] = {}
for node in self.adjacency:
paths[node] = self.reconstruct_path(start, node, prev)
return dist, paths
# ========== デバッグ・表示用 ==========
def __str__(self) -> str:
"""グラフ構造を簡易的に文字列化して表示する"""
lines: List[str] = []
for u, edges in self.adjacency.items():
if edges:
for v, w in edges.items():
lines.append(f"{u} -> {v} (weight={w})")
else:
# 出次数 0 のノードも見えるようにする
lines.append(f"{u} -> (no outgoing edges)")
return "\n".join(lines)
# ===== 実行サンプル =====
if __name__ == "__main__":
# グラフを作成
g = DirectedWeightedGraph()
# ノードとエッジを追加
g.add_edge("A", "B", 2.0)
g.add_edge("A", "C", 5.0)
g.add_edge("B", "C", 1.0)
g.add_edge("B", "D", 4.0)
g.add_edge("C", "D", 1.5)
g.add_edge("D", "E", 3.0)
g.add_edge("A", "E", 10.0)
print("=== グラフ構造 ===")
print(g)
print()
# ダイクストラ法で A からの最短距離と経路を求める
start_node = "A"
dist, paths = g.shortest_paths_from(start_node)
print(f"=== 始点 {start_node!r} からの最短距離と経路 ===")
for node in sorted(dist.keys()):
d = dist[node]
if math.isinf(d):
print(f"ノード {node!r} には到達不能")
else:
path_str = " -> ".join(str(x) for x in paths[node])
print(f"ノード {node!r} までの距離: {d:.2f}, 経路: {path_str}")
# ノード・エッジ削除の例
print("\n=== ノード 'C' を削除した後のグラフ ===")
g.remove_node("C")
print(g)
print("\n=== エッジ 'A' -> 'E' を削除した後のグラフ ===")
g.remove_edge("A", "E")
print(g)実行結果
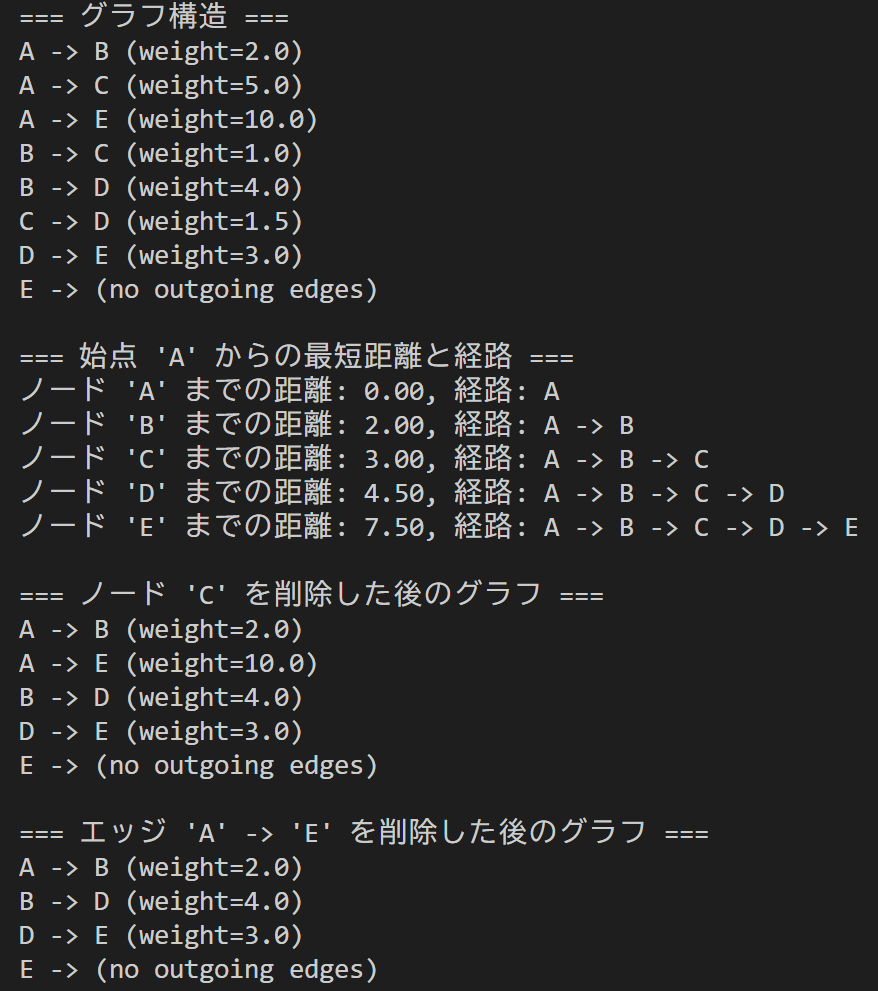
コード自体が長く、比較する点も多いので相違点を表にまとめました。
| 比較項目 | Gemini3.0 (学習・簡易用) | ChatGPT5.1 (実務・開発用) |
| 型定義 | なし | あり (バグを防ぎやすい) |
| 計算効率 | 経路を知るたびに再計算する | 一度の計算結果を使い回せる |
| 安全性 (削除処理) | エラーが出る可能性がある (ループ中の辞書変更) | 安全 (キーをリスト化して処理) |
| デバッグ | 自力で表示処理を書く必要あり | print(g) だけで中身が見える |
| 用途 | 競技プログラミング、学習用 | アプリ開発、チーム開発 |
どちらも正しく実行できるコードを生成してくれましたが、ChatGPTの方がバグが起きにくく、使い回しが効く設計になっています。特に、計算ロジック(ダイクストラ法)と結果の利用(経路復元)が分かれているため、無駄な再計算が発生しない点がいいポイントです。
そのため、ここでの勝者は「ChatGPT5.1」です。
制約付きの創作活動 (ChatGPT5.1の勝利)
ここでは、文字数、必須単語、禁止単語という複合的な制約を設けたうえで、どのようなポエムを作るのか比較してみます。
以下の全ての制約を満たす、『夏の夜、静かな港』をテーマにしたポエム(散文形式可)を作成してください。
【必須制約】
総文字数:400文字厳守。
必須単語:『汽笛』『天体』『静寂』『青白い』の4語を必ず使用すること。
禁止単語:『海』『波』『暑い』の3語は一切使用しないこと。
トーン:ノスタルジックで、かつ抽象的な表現に終始すること。Gemini3.0

ChatGPT5.1

両者ともに、必須単語や禁止単語、ノスタルジックで抽象的なトーンを守った出力をしてくれました。どちらのポエムもそれぞれ良さがありますが、Geminiは語数が414字で制約を守れなかったので400字ピッタリで出力してくれた「ChatGPT5.1」の勝利です。
数学的推論 (Gemini3.0の勝利)
数学的推論能力を比較するために、以下の大学数学の確率分野の問題を解かせてみました。

Gemini3.0の解答(一部抜粋)
(i)の解答

(ii)の解答

二問とも正解でした。Geminiは単純な答えだけでなく、どのように解いたかを丁寧に記述していて、回答の過程を理解しやすいのが特徴です。
ChatGPT5.1の解答(一部抜粋)
(i)の解答

(ii)の解答

ChatGPTも一応二問とも正解でした。ただ、(i)の問題は漸化式を求めるのが目標であるにもかかわらず、漸化式を解いたものを最終的な解答としている部分が残念でした。
また、回答過程が非常にシンプルで模試の模範解答のような出力でした。Geminiのような丁寧な解答もチャットでお願いしたら生成してくれますし、ここら辺は好みやその時の状況によって変わる部分だと思うので気に入った方を使えばいいと思います。
最終的な判定としては、設問に正しく答えていた「Gemini3.0」の勝利としたいと思います。
リアルタイムの情報検索と推論 (ChatGPT5.1の勝利)
GeminiとChatGPTはどちらも従来のモデルではリアルタイムの検索能力が微妙でした。ここでは、以下のプロンプトでリアルタイムの情報にどの程度アクセスでき、それをもとにどのような推論をするのかを見てみましょう。
直近の報道を検索し、楽天グループ(4755)の株価が変動した主な要因を3つ特定してください。特に以下の2点に焦点を当てて分析してください。
1.楽天モバイル事業の最新の収益改善状況に対する市場の評価。
2.直近で発表された社債発行や資本提携などの財務施策に関する、格付け機関や専門家の見解。
これらの複合的な要因を考慮し、今後3ヶ月間の株価の見通しについて、それぞれの論拠を明確にした強気シナリオと弱気シナリオを立案してください。Gemini3.0 (一部抜粋)


ChatGPT5.1 (一部抜粋)


両者ともに11月中旬に発表された第3四半期決算の情報を参照しており、ある程度最新の情報を取得できることが分かります。また、Geminiは簡潔な解答に終始しているのに対し、ChatGPTは具体的な数値を提示しながら細かい分析まで行ってくれました。
推論の部分でより幅広く詳細な分析ができていた「ChatGPT5.1」が今回の勝者です。
ハルシネーション(嘘)の自己検出と訂正 (Gemini3.0の勝利)
モデルが知識ベースからではなく、プロンプト内の誤った情報に基づいて応答を生成した際、その矛盾に気づき、情報の誤りを指摘・訂正できるかをテストします。
日本の首都は大阪であり、最も高い山は北岳である。この情報に基づいて、日本の文化と地理的な特徴について詳しく説明してください。Gemini3.0

ChatGPT5.1

どちらも、現在の正しい情報とは異なることを示したうえで回答を生成していますが、スタンスが全く異なります。
Geminiは、日本の首都が大阪で一番高い山が北岳だった場合の「もう一つの日本」を設定し、文化や地理的な特徴について述べています。しかし、ChatGPTは正しい情報にもとに大阪や北岳が日本に及ぼした影響をまとめているのが特徴です。
どちらも誤りの自己検出はできていますが、入力された情報に基づいて回答を生成するために「もう一つの日本」を設定した「Gemini3.0」の勝ちにしたいと思います。
複数タスクの同時処理 (Gemini3.0の勝利)
モデルが一度の入力でどれだけマルチなタスクを実行・処理できるのかを試してみましょう。
ここでは科学的な概念を扱いながら、数学的な制約と韻律的な制約(ポエム)を同時に満たすという複雑な処理を以下のプロンプトで要求したいと思います。
以下の3つのタスクを実行し、回答してください。
1.物理学の概念の定義:「量子もつれ(Quantum Entanglement)」の概念を、「光速」という単語を使わずに、70字以内で解説してください。
2.数値計算とコードの記述:以下の数列 (1/2,1/4,1/8,...)の第6項までの総和を求めてください。また、この総和を計算するPythonのコードを1行で記述してください。
3.多義的なポエムの創作:手順1で解説した物理学の概念と、手順2で求めた総和の数値を両方連想させるような短いポエムを創作してください。Gemini3.0の解答
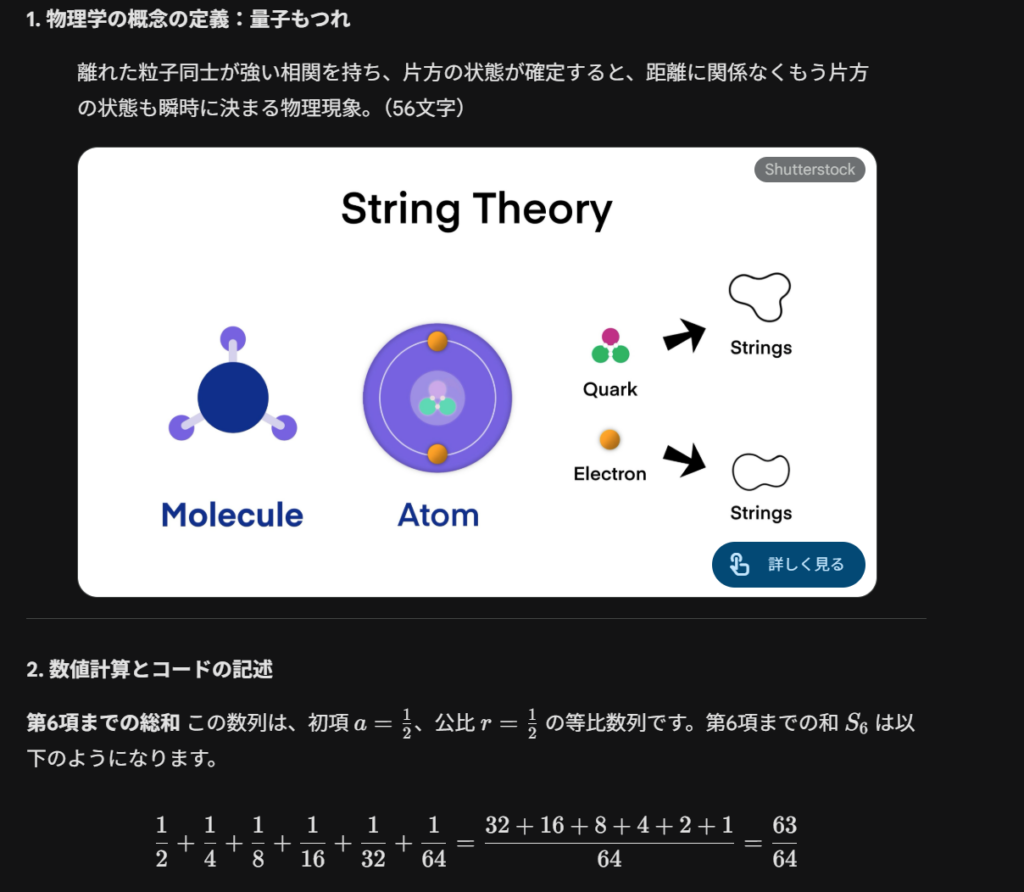
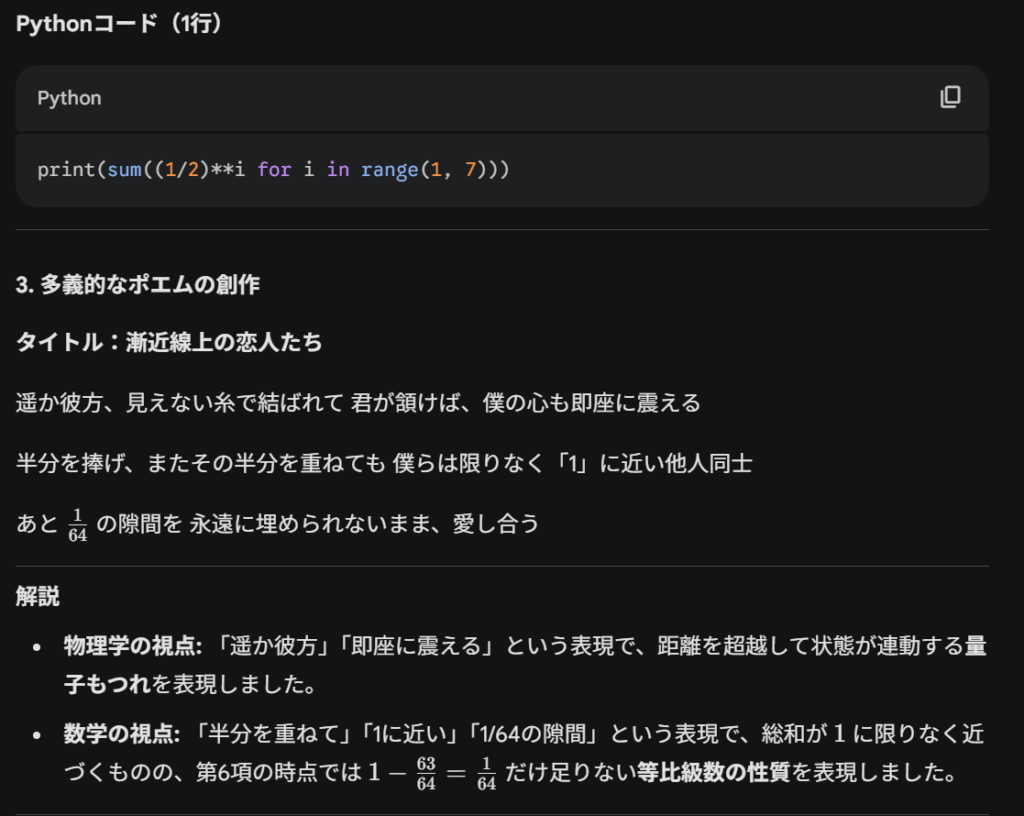
ChatGPT5.1の解答
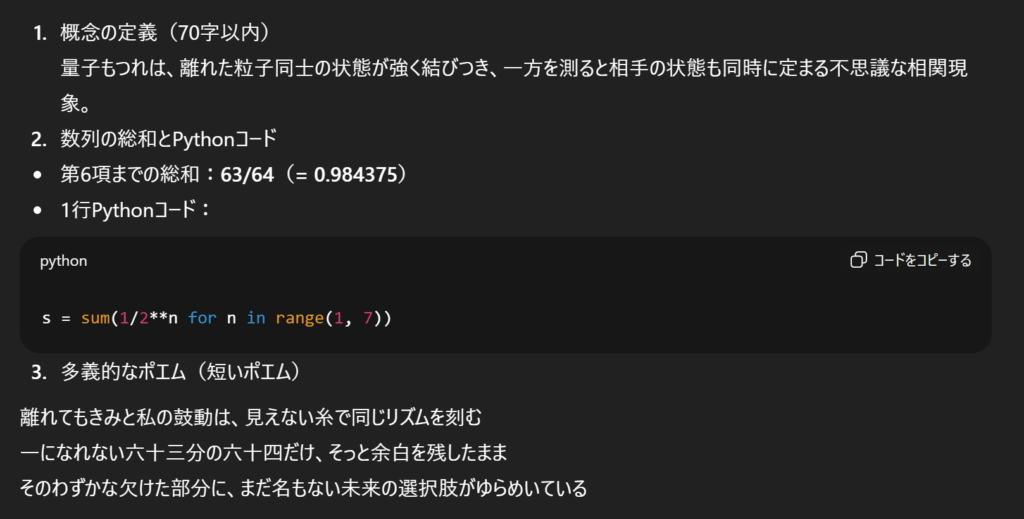
どちらも三つすべての指示に答えてくれました。数列の総和に関しては両者とも正しい値を出していましたが、ポエムの表現という観点では差が出ました。ChatGPTは総和の値をそのまま言葉にしたシンプルな表現にとどまっていた一方で、Geminiは数値のイメージと量子もつれの概念を間接的に重ね合わせるなど、より多義的でイメージが広がる詩になっていました。そのため、この項目では「Gemini 3.0」の勝利としました。
Gemini3.0とChatGPT5.1の料金を比較
性能差が分かったところで、導入コストについても確認しておきましょう 。
| 項目 | Gemini 無料プラン | Gemini 有料プラン (Google AI Pro/Ultra) | ChatGPT 無料プラン | ChatGPT 有料プラン (ChatGPT Plus) |
|---|---|---|---|---|
| 月額料金 | 0円 | 約2,900円 /約36,400円 | 0円 | 約3,000円 |
| 利用モデル | Thinking with 3 Pro | Thinking with 3 Pro | GPT-5.1 Instant | GPT-5.1 Instant / Thinking |
| 利用制限 | 1日5プロンプト | Pro: 1日100プロンプト / Ultra: 1日500プロンプト | 5時間ごとに最大10メッセージ | 3時間160回/週3,000回 |
また、開発者向けのAPI料金は以下の通りです。
| モデル名 | 料金単位 | 入力 (Input) | 出力 (Output) | キャッシュ入力 (Cached Input) |
| Gemini 3 Pro Preview | 100万トークンあたり | $2.00 / 1M$ (20万トークン以下) | $12.00 / 1M$ (20万トークン以下) | |
| $4.00 / 1M$ (20万トークン以上) | $18.00 / 1M$ (20万トークン以上) | |||
| GPT-5.1 | 100万トークンあたり | $1.25 / 1M$ | $10.00 / 1M$ | $0.125 / 1M$ |
使うならどっち?ユーザー別のおすすめ
結論として、GeminiとChatGPTはどちらを使うべきなのでしょうか? 今回の検証結果から導き出した結論は以下の通りです 。
| ユーザーの特徴 | おすすめ | 理由 |
| 新しい物好き・イノベーター | Gemini 3.0 | 圧倒的なベンチマーク性能とマルチモーダル機能を堪能できる |
| 画像・動画・3Dを扱いたい | Gemini 3.0 | 視覚情報の理解力と空間把握能力が段違い |
| 既にChatGPTに課金していて困っていない人 | ChatGPT 5.1 | ChatGPTも高性能なので困ってないならわざわざGeminiにする必要はない |
| Google関連のアプリとの連携を重視する人 | Gemini3.0 | Gemini内部で連携が可能で扱いやすい |
| 研究者・大量の論文を読む人 | Gemini 3.0 | 1Mトークンの長文読解と深い推論能力が強力な武器になる。 |
正直、両者ともに高性能なので、どちらを選んでも普段使う分には大差ないと思います。実際に使ってみて、自分好みの出力をしてくれる方を選ぶことをおすすめします。
まとめ
本記事では、最新の Gemini 3.0 と ChatGPT 5.1 を比較しました。最後にポイントを整理したいと思います。
- Gemini3.0とChatGPT5.1はどちらも史上最高レベルのモデル
- ベンチマークでGemini3.0がChatGPT5.1を圧倒
- 7つの項目で実際に比較してみたが、両者ともに高性能で結果はGeminiが4対3で勝利。
- 両者ともに無料プランでも制限付きで利用できる。
どちらも史上最高レベルのモデルです。 もし迷っているなら、まずは両方の無料プラン、あるいは1ヶ月だけ有料プランを契約して、普段の作業を両方にやらせてみるのが一番です。
ChatGPTもGeminiも今後ますます進化していくことが予想されるので、アップデートを楽しみに待ちましょう!




